You might enjoy reading Adam Diamant’s article on the value of Excel for teaching MBA students:
Author: Andrew Mason (Team OpenSolver)
We are hiring!
My department is currently recruiting for a Lecturer/Senior Lecturer position. More details at https://www.access-sciencejobs.uk/job/332043/lecturer-senior-engineering-australasia
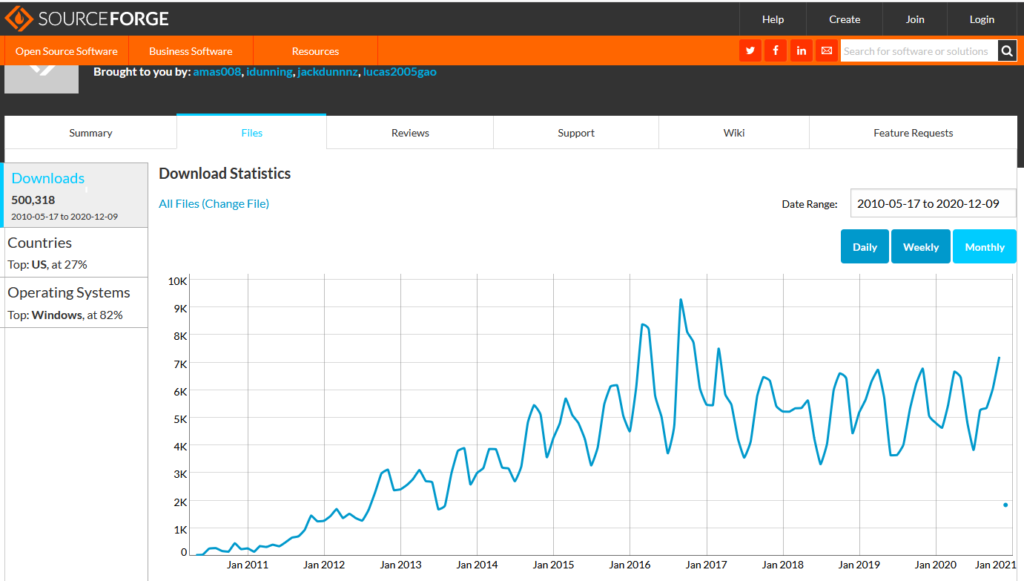
500,000 downloads
Today (10 Dec 2020) was a big day for OpenSolver, as we rolled past the 500,000 downloads count. Many thanks to all our Engineering Science (University of Auckland) students who have worked on this over the last decade, with a really large thank you to Jack Dunn for his major contributions over many years (including creating the Mac version). The community feedback is also much appreciated – thanks for letting us know of issues and suggesting enhancements. Cheers, Andrew
OpenSolver for Mental Health
ResearchGate let me know today that OpenSolver is being used to help allocate mental health personnel in the US Navy.
New Support Site for CBC Solver
Most of our OpenSolver users choose the standard integer programming solver, CBC (which is the default option). COIN-OR, the non-profit who support and develop CBC, have just announced a new support forum for CBC users. (This is a beta test of the new GitHub discussion forums being developed.) This is the best place for advanced users to take technical questions, such as queries about CBC parameters (which OpenSolver supports). Andrew
OpenSolver 2.9.3 Beta Release
Hi everyone,
We have now released OpenSolver 2.9.3 for beta testing! You can download this new version of OpenSolver on https://sourceforge.net/projects/opensolver/files/. Below are the release notes that cover the changes made in this new version of OpenSolver:
v2.9.3 – 2020/03/02
- Added support for using Gurobi 9.0
- Added a temp fix for running consecutive operations on Excel64bit
v2.9.2 – 2019-02-04
- Add support for NEOS CPLEX as a new solver.
- Add import LP file feature.
- Add Examples files and submenu.
- Fix memory error when solving consecutive non-linear models in 64bit.
As always, we welcome any feedback! Please comment below if it works ok, or if there are any issues encountered, or if you have any questions regarding the new release. Thanks!
OpenSolver for Google Sheets currently down for new users
12 Feb 2020: It was raised to us that OpenSolver for GoogleSheets is still unaccessible to new users. We are now able to replicate this bug. From our tests, new user accounts are able to install OpenSolver for Google Sheets as an Add-on from Chrome Web Store. However, the “Sign in with Google is temporarily disabled for this app” screen will still show up when trying to open the sidebar from the ribbon. We are very sorry for the inconvenience and we have contacted Google regarding this issue. We need to wait for Google’s response on this, therefore we are unsure of when this problem will be fixed.
10 Feb 2020: This is no longer the case! OpenSolver for Google Sheets is now back online for new user installations. The “app isn’t verified” screen will no longer show up for new installations. We have also updated our privacy policy to align with Google’s requirements. For more information on the usage of Google OAuth scopes please visit our OpenSolver for Google Sheets page and our Privacy Policy page.
Original post: Changes made by Google mean that OpenSolver for Googlesheets is currently not working for new users who want to add it to their Googlesheets. (Apparently the first 100 users each month can sign in, but then further sign ins are blocked by Google.) We are working on fixing this, But we don’t know how long it will take, sorry. We suggest you use OpenSolver for Excel until we get it working properly for Googlesheets.
Sorry for the inconvenience.
Cheers,
Andrew
Want to optimise your Google ad allocation?
Google has a nice article here, that includes a recommendation to use OpenSolver. Enjoy!
OpenSolver for Ecological Conservation
We justc ame across an interesting article using OpenSolver to help develop optimal policies for conservation.
https://esajournals.onlinelibrary.wiley.com/doi/full/10.1002/ecs2.2596
Commonalities in stream connectivity restoration alternatives: an attempt to simplify barrier removal optimization
Ryan A. McManamayJoshuah S. PerkinHenriette I. Jager First published: 07 February 2019 https://doi.org/10.1002/ecs2.2596
https://esajournals.onlinelibrary.wiley.com/doi/full/10.1002/ecs2.2596

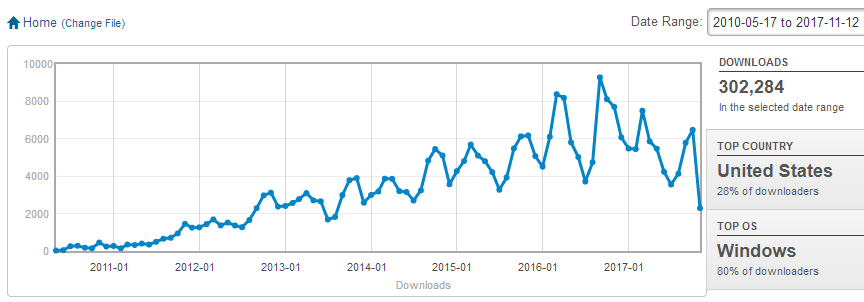
300k Downloads
OpenSolver reached another download milestone this month. If my car had reached 300,000 on the dial, I’d be looking at getting a new one. Fortunately, OpenSolver gets better with age.
Thank to all our users for their support.
Andrew
Good overview of optimisation software
There’s a great overview of software available for optimisation in Optima (volume 103, 2017), the Mathematical Optimization Society Newsletter.
250k milestone
Today the download odometer rolled past another milestone:
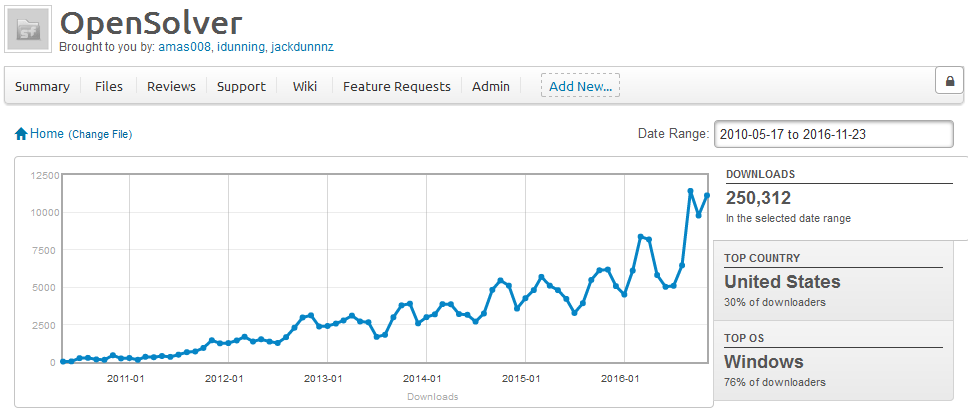
Thanks to all our users and our development team (and most recently Jack Dunn) for supporting OpenSolver for the last 6 years. None of this would have been possible without the solvers from COIN-OR; thanks to John Forrest and Ted Ralphs for the many years of CBC development, without which the OpenSolver project would never have started.
Andrew
MIT Analytics MOOC using OpenSolver
MIT have recently started a free Analytics MOOC, run by Jim Orlin, using OpenSover for Excel and OpenSolver for Google Sheets. (It also uses Julia and JUMP, which our SolverStudio system supports.) I recommend this course for all new users. Andrew
Fantasy Football – from OpenSolver to Cloud optimiser
This blog by Derek Nelson shows how he built an OpenSolver model for fantasy football that worked well for him. “My optimizer was created using Excel with the Open Solver add-in. This worked for me and the results were good. Namely, I had the highest projected points for my teams at the start of the season in both leagues I played in (the best you can hope for in the draft, in my opinion), and I ended the season by winning one league and placing second in the other.”
Derek has now gone on to create a cloud-based version of this. This work is an interesting optimisation-based project.
Sudoku and OpenSolver
As this video shows, yes, OpenSolver can solve Sudoku…
